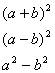| | | |
Data |
Temat lekcji / Kryteria sukcesu |
Liczba godzin |
Wymagania z podstawy programowej |
II SEMESTR 2015/2016 |
Powtórzenie zakresu treści matematyki szkoły ponadgimnazjalnej |
80 |
P - zakres podstawowy,
R- zakres rozszerzony |
15.02.2016
poniedziałek |
-Obliczanie wartości wyrażeń arytmetycznych.
-Pierwiastki dowolnego stopnia.
-Prawa działań na pierwiastkach.
-Potęgi o wykładnikach wymiernych.
-Prawa działań na potęgach o wykładnikach wymiernych.
Liczby rzeczywiste - działania na liczbach-video
Potęga o wykładniku wymiernym-video
DZIAŁANIA NA LICZBACH -potęgi, pierwiastki, ułamki, procenty ZADANIA
 Potęgi i pierwiastki
 1. Sprawdź czy umiesz? - rozwiąż zadania i sprawdź odpowiedzi
 e-podręcznik- 4.5. Potęgi o wykładniku wymiernym |
3 |
P - zakres podstawowy,
Uczeń:
1. 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg);
1. 2) oblicza wartości wyrażeń arytmetycznych (wymiernych);
1. 3) posługuje się w obliczeniach pierwiastkami dowolnego stopnia i stosuje prawa działań na pierwiastkach;
1. 4) oblicza potęgi o wykładnikach wymiernych i stosuje prawa działań na potęgach o wykładnikach wymiernych; |
17.02.2016
sroda |
-Logarytmy.
-Wzory na logarytm iloczynu, logarytm ilorazu i logarytm potęgi o wykładniku naturalnym.
Logarytmy - najważniejsze wiadomości
Logarytmy- zadania maturalne-video
LOGARYTMY - ZADANIA
 Działania na logarytmach (dziesietnych)
 Elementarne równanie wykładnicze i wykorzystanie potęgi. Brakujący wykładnik potęgi.
 Logarytmy
2. Sprawdź czy umiesz?- rozwiąż zadania i sprawdź odpowiedzi
e-podręcznik - logarytmy |
3 |
P - zakres podstawowy,
Uczeń:1. 6) wykorzystuje definicję logarytmu i stosuje w obliczeniach wzory na logarytm iloczynu, logarytm ilorazu i logarytm potęgi o wykładniku naturalnym; |
19.02.2016
piątek |
-Błąd bezwzględny i błąd względny przybliżenia. -Przedziały liczbowe.
-Wykorzystanie podstawowych własności potęg w innych dziedzinach wiedzy.
-Obliczenia procentowe - zadanie domowe do opracowania metodą projektu e-podrecznik zadania + tu materiał do opracowania
Procenty - podwójne obniżki ceny - metody rozwiązywania-video
Procenty - zadanie
Zadanie -błąd względny
zadanie2-błąd względny
3. Sprawdź czy umiesz?- rozwiąż zadania i sprawdź odpowiedzi |
2 |
P - zakres podstawowy,
Uczeń:
1. 5) wykorzystuje podstawowe własności potęg (również w zagadnieniach związanych z innymi dziedzinami wiedzy, np. fizyką, chemią, informatyką);
1. 7) oblicza błąd bezwzględny i błąd względny przybliżenia;
1. 8) posługuje się pojęciem przedziału liczbowego, zaznacza przedziały na osi liczbowej;
1. 9) wykonuje obliczenia procentowe, oblicza podatki, zysk z lokat (również złożonych na procent składany i na okres krótszy niż rok). |
22.02.2016
poniedziałek |
PP-1. Sprawdzian - liczby rzeczywiste w tym zadania maturalne(1h)
-Podstawowe wiadomości o wyrażeniach algebraicznych, obliczanie wartości wyrażeń algebraicznych.
-Wzory skróconego mnożenia.
 Dobierz odpowiednie wyrażenie algebraiczne
 dopasuj odpowiednie wyrażenie
Jak sobie radzić ze wzorami skróconego mnożenia? Część I. Kwadrat sumy
Jak sobie radzić ze wzorami skróconego mnożenia? Część II. Kwadrat różnicy
Jak sobie radzić ze wzorami skróconego mnożenia? Część III. Różnica kwadratów
Jak sobie radzić ze wzorami skróconego mnożenia? Część IV. Przykłady zastosowań
4. Sprawdź czy umiesz?- rozwiąż zadania i sprawdź odpowiedzi
działania na wyrażeniach algebraicznych |
3 |
P - zakres podstawowy,
Uczeń:
2. 1) używa wzorów skróconego mnożenia |
24.02.2016
sroda |
-Równania i nierówności liniowe z jedną niewiadomą.
-Sposoby rozwiązywania układów równań liniowych.
Zadanie - Zbiór rozwiązań nierówności -video
zadanie - nierówność liniowa
Układy równań liniowych cz1. Układ oznaczony.Dwie metody i ilustracja geometryczna
Układy równań liniowych cz2. Układ nieoznaczony. Dwie metody i ilustracja geometryczna
Układy równań liniowych cz3. Układ sprzeczny. Dwie metody i ilustracja geometryczna
ZADANIA - równania liniowe i kwadratowe
ZADANIA-nierówności liniowe i kwadratowe
5. Sprawdź czy umiesz?-rozwiąż zadania i sprawdź odpowiedzi |
3 |
P - zakres podstawowy,
Uczeń:
3. 1) sprawdza, czy dana liczba rzeczywista jest rozwiązaniem równania lub nierówności;
3. 2) wykorzystuje interpretację geometryczną układu równań pierwszego stopnia z dwiema niewiadomymi;
3. 3) rozwiązuje nierówności pierwszego stopnia z jedną niewiadomą; |
26.02.2016
piątek |
-Równania i nierówności kwadratowe z jedną niewiadomą.
Równania kwadratowe niezupełne-video
Nierówności kwadratowe
Nierówność kwadratowa - omówienie wszystkich przypadków-video
Równania kwadratowe - metoda na rozwiązanie w głowie w 3 sekundy!-video
 Równania kwadratowe
Równania kwadratowe
Nierówności kwadratowe
6. Sprawdź czy umiesz?-rozwiąż zadania i sprawdź odpowiedzi |
2 |
P - zakres podstawowy,
Uczeń:
3.4) rozwiązuje równania kwadratowe z jedną niewiadomą;
3.5) rozwiązuje nierówności kwadratowe z jedną niewiadomą; |
29.02.2016
poniedziałek |
-Wykorzystanie definicji pierwiastka do rozwiązywania równań typu .
-Wykorzystanie własności iloczynu do rozwiązywania równań.
-Działania na wyrażeniach wymiernych.
-Proste równania wymierne.
Wielomian w postaci iloczynowej - zadanie
Równania wymierne - metoda rozwiązywania
Równania wymierne ; 
 Równania typu x(x+1)(x-3)=0
7. Sprawdź czy umiesz?rozwiąż zadania i sprawdź odpowiedzi |
3 |
P - zakres podstawowy,
Uczeń:
3.6) korzysta z definicji pierwiastka do rozwiązywania równań typu 
3.7) korzysta z własności iloczynu przy rozwiązywaniu równań typu x(x+1)(x-1)=0 ;
3.8) rozwiązuje proste równania wymierne, prowadzące do równań liniowych lub kwadratowych, np.
 ;  |
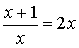02.03.2016
sroda |
PP-2,3. sprawdzian - równania i nierówności w tym zadania maturalne (1h)
-Sposoby określania funkcji.
-Obliczanie wartości funkcji dla danego argumentu.
-Obliczanie argumentu funkcji dla danej wartości.
-Odczytywanie własności funkcji z wykresu.
-Przekształcanie wykresu funkcji .
Własności funkcji odczytane z wykresu
ZADANIA-dziedzina i zbiór wartości funkcji, miejsca zerowe, wykres funkcji, zadania z parametrem
Przekształcenia wykresów funkcji
Przekształcenia wykresu funkcji. Przesunięcie wykresu podstawowego
Przekształcenia wykresu funkcji. Minusy we wzorze funkcji. symerie.
 Odczytaj z wykresu zbiór wartości
8. Sprawdź czy umiesz?rozwiąż zadania i sprawdź odpowiedzi |
3 |
P - zakres podstawowy,
Uczeń:
4.1) określa funkcje za pomocą wzoru, tabeli, wykresu, opisu słownego;
4.2)oblicza ze wzoru wartość funkcji dla danego argumentu. Posługuje się poznanymi metodamirozwiązywania równań do obliczenia, dla jakiego argumentu funkcja przyjmuje daną wartość;
4.3) odczytuje z wykresu własności funkcji (dziedzinę, zbiór wartości, miejsca zerowe, maksymalne przedziały, w których funkcja
maleje, rośnie, ma stały znak; punkty, w których funkcja przyjmuje w podanym przedziale wartość największą lub najmniejszą);
4.4)na podstawie wykresu funkcji y =f(x) szkicuje wykresy funkcji y = f(x + a), y = f(x)+ a, y = –f(x), y =f(–x); |
04.03.2016
piątek
|
-Wykres funkcji liniowej.
-Wyznaczanie wzoru funkcji liniowej.
-Współczynniki we wzorze funkcji liniowej
-Układ równań liniowych - ilustracja geometryczna
 Milionerzy - funkcja liniowa
Funkcja liniowa - praktyczny sposób na rysowanie wykresu
Wyznacz wzór funkcji liniowej- zadanie
Wykres i wzór w postaci kierunkowej
Równanie kierunkowe prostej
ZADANIA - wykres funkcji liniowej, wyznaczanie równania prostej, proste równoległe i prostopadłe.
Układy równań liniowych cz1. Układ oznaczony.Dwie metody i ilustracja geometryczna
Układy równań liniowych cz3. Układ sprzeczny. Dwie metody i ilustracja geometryczna
9. Sprawdź czy umiesz?rozwiąż zadania i sprawdź odpowiedzi |
2 |
P - zakres podstawowy,
Uczeń:
4.5) rysuje wykres funkcji liniowej, korzystając z jej wzoru;
4. 6) wyznacza wzór funkcji liniowej na podstawie informacji o funkcji lub o jej wykresie;
4. 7) interpretuje współczynniki występujące we wzorze funkcji liniowej;
3. 2) wykorzystuje interpretację geometryczną układu równań pierwszego stopnia z dwiema niewiadomymi; |
07.03.2016
poniedziałek |
-Funkcja kwadratowa.
-Wyznaczanie wzoru funkcji kwadratowej na podstawie informacji o funkcji lub jej wykresie.
-Interpretacja współczynników występujących we wzorze funkcji kwadratowej w postaci kanonicznej, ogólnej i iloczynowej.
-Wartość najmniejsza i wartość największa funkcji kwadratowej w przedziale zamkniętym.
Funkcja kwadratowa - wszystko co warto wiedzieć-video
Funkcja kwadratowa - zadania maturalne
Funkcja kwadratowa - postać ogólna, kanoniczna i iloczynowa
ZADANIA - wykres funkcji kwadratowej, miejsca zerowe, wierzchołek, zadania tekstowe.
 Funkcja kwadratowa
Zadanie: Oblicz najmniejszą i największą wartość funkcji kwadratowej f(x) = x^2 - 6x + 3 w przedziale
(domkniętym) [0, 4]
10. Sprawdź czy umiesz? rozwiąż zadania i sprawdź odpowiedzi |
3 |
P - zakres podstawowy,
Uczeń:
4. 8) szkicuje wykres funkcji kwadratowej, korzystając z jej wzoru;
4. 9) wyznacza wzór funkcji kwadratowej na podstawie pewnych informacji o tej funkcji lub o jej wykresie;
4. 10) interpretuje współczynniki występujące we wzorze funkcji kwadratowej w postaci kanonicznej, w postaci ogólnej i w postaci iloczynowej (o ile istnieje);
4.11) wyznacza wartość najmniejszą i wartość największą funkcji kwadratowej w przedziale domkniętym;
|
09.03.2016
sroda
|
kartkówka - funkcja kwadratowa
-Wykorzystanie własności funkcji liniowej i kwadratowej w kontekście praktycznym.
-Wykres i własności funkcji f (x)= a/x .
-Wielkości wprost i odwrotnie proporcjonalne.
-Funkcja wykładnicza i jej własności.
-Wykorzystanie funkcji wykładniczej w kontekście praktycznym.
Funkcja wymierna i własności
Wielkości odwrotnie proporcjonalne w zadaniach
funkcja wykładnicza do opisu zjawisk-zadanie1
funkcja wykładnicza do opisu zjawisk-zadanie2
11. Sprawdź czy umiesz? rozwiąż zadania i sprawdź odpowiedzi
Zadania z treścią |
3 |
P - zakres podstawowy,
Uczeń:
4.12) wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp. (także osadzonych w kontekście praktycznym);
4.13) szkicuje wykres funkcji f(x) = a/x dla danego a, korzysta ze wzoru i wykresu tej funkcji do interpretacji zagadnień związanych z wielkościami odwrotnie proporcjonalnymi;
4. 14) szkicuje wykresy funkcji wykładniczych dla różnych podstaw;
|
11.03.2016
piątek |
-Wykorzystanie własności funkcji liniowej i kwadratowej w kontekście praktycznym.
-Wykorzystanie funkcji wykładniczej w kontekście praktycznym.
Zadania z treścią
Zadanie - video
Zadania z treścią prowadzące do równań kwadratowych
11. Sprawdź czy umiesz? rozwiąż zadania i sprawdź odpowiedzi
Zadania z treścią |
1 |
P - zakres podstawowy,
Uczeń:
4.12) wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp. (także osadzonych w kontekście praktycznym);
4. 15) posługuje się funkcjami wykładniczymi do opisu zjawisk fizycznych, chemicznych, a także w zagadnieniach osadzonych w kontekście praktycznym. |
|
Rozwiąż zadania- przed pracą klasową |
zad.
dom. |
jak wyżej |
14.03.2016
poniedziałek |
PRACA KLASOWA - LICZBY RZECZYWISTE, RÓWNANIA, NIERÓWNOŚCI I FUNKCJE |
2h |
jak wyżej |
14.03.2016
poniedziałek
16.03.2016
sroda
|
Ciągi liczbowe
-Wyznaczanie wyrazów ciągu określonego wzorem ogólnym.
Ciąg arytmetyczny i ciąg geometryczny - własności
-Badanie, czy dany ciąg jest arytmetyczny lub geometryczny.
-Zastosowanie wzoru na n-ty wyraz i na sumę n początkowych wyrazów ciągu arytmetycznego.
-Zastosowanie wzoru na n-ty wyraz i na sumę n początkowych wyrazów ciągu geometrycznego.
Ciąg arytmetyczny - najważniejsze wiadomości-video
Ciąg geometryczny - najważniejsze wiadomości-video
ZADANIA - CIĄGI-wzór ogólny ciągu, ciąg arytmetyczny, ciąg geometryczny.
Zastosowanie ciągów - zadanie
12. Sprawdź czy umiesz? Ciągi liczbowe, ciag arytmetyczny, ciąg geometryczny |
4 |
P - zakres podstawowy,
Uczeń:
5.1) wyznacza wyrazy ciągu określonego wzorem ogólnym;
5.2) bada, czy dany ciąg jest arytmetyczny lub geometryczny;
5. 3) stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu arytmetycznego;
5. 4) stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu geometrycznego. |
18.03.2016
piątek |
PP-5. sprawdzian - ciągi w tym zadania maturalne (1h)
Twierdzenie Pitagorasa i funkcje trygonometryczne w trójkącie prostokątnym
zadanie- Przyprostokątne trójkąta prostokątnego maja długości 8 i 6, sinus większego z kątów ostrych tego trójkąta jest równy.
13. Sprawdź czy umiesz? Twierdzenie Pitagorasa i funkcje trygonometryczne w trójkącie prostokatnym. |
2 |
Uczeń:
G - zna i stosuje twierdzenie Pitagorasa
P- zna definicje funkcji sinus, cosinus i tangens
-stosuje w/w funkcje do rozwiązaywania trójkatów prostokatnych. |
21.03.2016
poniedziałek
23.03.2016
środa
|
Funkcje trygonometryczne
-Wykorzystanie definicji i wyznaczanie wartości sinus, cosinus i tangens kątów o miarach od 0 do 180.
-Wykorzystywanie przybliżonych wartości funkcji trygonometrycznych (odczytywanych z tablic lub obliczonych za pomocą kalkulatora).
-Obliczanie miary kąta ostrego, dla której funkcja trygonometryczna przyjmuje daną wartość (miarę dokładną albo korzystając z tablic lub kalkulatora - przybliżoną).
-Zastosowanie prostych zależności między funkcjami trygonometrycznymi: sin2a + cos2a = 1 oraz sin(90 - a) = cosa.
-Wyznaczanie wartości funkcji tego samego kąta, znając wartość jednej z nich.
ZADANIA- TRYGONOMETRIA-sin, cos i tg w trójkącie prostokątnym, podstawowe wzory i zależności trygonometryczne
Trygonometria - typowe zadanie i różne podejścia
14. Sprawdź czy umiesz? Trygonometria |
5
|
P - zakres podstawowy,
Uczeń:
6.1) wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus
i tangens kątów o miarach od 0° do 180°;
6.2) korzysta z przybliżonych wartości funkcji trygonometrycznych
(odczytanych z tablic lub obliczonych za pomocą kalkulatora);
6. 3) oblicza miarę kąta ostrego, dla którego funkcja trygonometryczna
przyjmuje daną wartość (miarę dokładną albo - korzystając z tablic
lub kalkulatora - przybliżoną);
6.4) stosuje proste zależności między funkcjami trygonometrycznymi: ; 
, oraz  ;
6. 5) znając wartość jednej z funkcji: sinus lub cosinus, wyznacza wartości pozostałych funkcji tego samego kąta ostrego. |
30.03.2016
środa
|
PP-6. sprawdzian - trygonometria w tym zadania maturalne (1h)
-Kąty.
-Czworokąty ichwłasności. Pola obwody
-Trójkąt i jego punkty charakterystyczne.
-Wykorzystanie własności funkcji trygonometrycznych w łatwych obliczeniach geometrycznych, w tym wzoru na pole trójkąta ostrokątnego o danych dwóch bokach i kącie między nimi.
ZADANIA-PLANIMETRIA-trójkąty, twierdzenie Pitagorasa, podobieństwo, kwadrat, trapez, romb, koło, okrąg, kąty wpisane i środkowe.
15 Sprawdź czy umiesz? PLANIMETRIA cz.1 |
3 |
P - zakres podstawowy,
Uczeń:
Oblicz pola i obwody wielokątów,
6.3) wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus
i tangens kątów o miarach od 0° do 180°;
|
01.04.2016
piątek |
-Stosowanie zależności między kątem środkowym i kątem wpisanym.
-Okręgi wpisane w wielokąt i opisane na wielokącie, w szczególności wpisane w trójkąt i opisane na trójkącie
-Rozpoznawanie trójkątów podobnych i wykorzystanie (także w kontekstach praktycznych) cech podobieństwa trójkątów.
-Własności stycznej do okręgu i własności okręgów stycznych.
-Figury przystające, w szczególności trójkąty przystające.
-Figury podobne.
-Wykorzystanie własności funkcji trygonometrycznych w łatwych obliczeniach geometrycznych, w tym wzoru na pole trójkąta ostrokątnego o danych dwóch bokach i kącie między nimi.
 Cechy przystawania i podobieństwa
 Podobieństwo trójkątów
 figury podobne
16 Sprawdź czy umiesz? PLANIMETRIA cz.2 |
2 |
P - zakres podstawowy,
Uczeń:
7. 1) stosuje zależności między kątem środkowym i kątem wpisanym;
7. 2) korzysta z własności stycznej do okręgu i własności okręgów
stycznych;
7. 3) rozpoznaje trójkąty podobne i wykorzystuje (także w kontekstach
praktycznych) cechy podobieństwa trójkątów;
6.3) wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus
i tangens kątów o miarach od 0° do 180°; |
04.04.2016
poniedziałek
06.04.2016
środa |
PP- 7. sprawdzian - planimetria w tym zadania maturalne (1h)
-Wyznaczanie równania prostej przechodzącej przez dwa punkty (w postaci kierunkowej lub ogólnej)
-Badanie równoległości i prostopadłości prostych na podstawie ich równań kierunkowych.
-Wyznaczanie równania prostej, która jest równoległa lub prostopadła do prostej danej w postaci kierunkowej i przechodzi przez dany punkt.
-Obliczanie współrzędnych punktu przecięcia dwóch prostych.
-Wyznaczanie współrzędnych środka odcinka. Obliczanie odległości dwóch punktów.
-Znajdowanie obrazów niektórych figur geometrycznych (punktu, prostej, odcinka, okręgu, trójkąta itp.) w symetrii osiowej względem osi układu współrzędnych i symetrii, środkowej względem początku układu współrzędnych.
Równanie kierunkowe prostej
ZADANIA -układ współrzędnych, długość odcinka, środek odcinka, symetralna odcinka, równanie prostej, punkt przecięcia prostych.
17 Sprawdź czy umiesz? GEOMETRIA ANALITYCZNA
|
1+2+3 |
P - zakres podstawowy,
Uczeń:
8. 1) wyznacza równanie prostej przechodzącej przez dwa dane punkty (w postaci kierunkowej lub ogólnej);
P - zakres podstawowy,
Uczeń:
8. 2) bada równoległość i prostopadłość prostych na podstawie ich równań kierunkowych;
8. 3) wyznacza równanie prostej, która jest równoległa lub prostopadła
do prostej danej w postaci kierunkowej i przechodzi przez dany punkt;
8. 4) oblicza współrzędne punktu przecięcia dwóch prostych;
8. 5) wyznacza współrzędne środka odcinka;
8. 6) oblicza odległość dwóch punktów;
8. 7) znajduje obrazy niektórych figur geometrycznych (punktu, prostej, odcinka, okręgu, trójkąta itp.) w symetrii osiowej względem osi układu współrzędnych i symetrii środkowej względem początku układu. |
08.04.2016
piątek |
PP-8. sprawdzian - geometria kartezjańska w tym zadania maturalne (1h)
-Średnia arytmetyczna, mediana, dominanta.
-Obliczanie średniej ważonej i odchylenia standardowego zestawu danych (także w przypadku danych odpowiednio pogrupowanych).
-Interpretowanie tych parametrów dla danych empirycznych.
ZADANIA -STATYSTYKA
18 Sprawdź czy umiesz? STATYSTYKA |
2 |
P - zakres podstawowy,
Uczeń:
10. 1) oblicza średnią ważoną i odchylenie standardowe zestawu danych (także w przypadku danych odpowiednio pogrupowanych), interpretuje te parametry dla danych empirycznych;
10. 2) zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania; |
11.04.2016
poniedziałek
|
-Doświadczenia losowe.
-Opisywanie doświadczeń losowych.
-Zliczanie obiektów w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych.
-Zastosowanie reguły mnożenia i reguły dodawania
-Obliczanie prawdopodobieństwa w prostych sytuacjach, stosując klasyczną definicję prawdopodobieństwa.
ZADANIA - reguła mnożenia, reguła dodawania, prawdopodobieństwo klasyczne
 Kombinatoryka
 Kombinatoryka
19 Sprawdź czy umiesz? PRAWDOPODOBIEŃSTWO |
3 |
P - zakres podstawowy,
Uczeń:
10. 3) oblicza prawdopodobieństwa w prostych sytuacjach, stosując klasyczną definicję prawdopodobieństwa. |
13.04.2016
środa |
PP-10. sprawdzian - prawdopodobieństwo w tym zadania maturalne (1h)
-Odcinki, kąty, przekroje figur przestrzennych.
-Obliczanie pól powierzchni i objętości graniastosłupów, ostrosłupów i brył obrotowych.
-Stosowanie trygonometrii do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości.
ZADANIA - graniastosłupy, ostrosłupy, bryły obrotowe
 Ostrosłup prawidłowy czworokątny - nazwy elementów
 objętość graniastosłupa
STEREOMETRIA W E-PODRĘCZNIKU
20 Sprawdź czy umiesz? STEREOMETRIA |
3 |
P - zakres podstawowy,
Uczeń:
9. 1) rozpoznaje w graniastosłupach i ostrosłupach kąty między odcinkami (np. krawędziami, krawędziami i przekątnymi, itp.), oblicza miary tych kątów;
9. 2) rozpoznaje w graniastosłupach i ostrosłupach kąt między odcinkami i płaszczyznami (między krawędziami i ścianami, przekątnymi i ścianami), oblicza miary tych kątów;
9. 3) rozpoznaje w walcach i w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między tworzącą a podstawą), oblicza miary tych kątów;
9. 4) rozpoznaje w graniastosłupach i ostrosłupach kąty między ścianami;
9. 5) określa, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną;
9. 6) stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości. |
15.04.2016
piątek |
Rozwiązywanie arkuszy maturalnych
Matura podstawowa - zadanie testowe |
2 |
Podstawa programowa - zakres podstawowy |
18.04.2016
poniedziałek |
Rozwiązywanie arkuszy maturalnych
MATURA 2016 - przydatne WZORY których nie ma w tablicach |
3 |
Podstawa programowa - zakres podstawowy |
20.04.2016
środa |
Rozwiązywanie arkuszy maturalnych |
3 |
Podstawa programowa - zakres podstawowy |
22.04.2016
piątek |
Rozwiązywanie arkuszy maturalnych |
2 |
Podstawa programowa - zakres podstawowy |
25.04.2016
poniedziałek |
Rozwiązywanie arkuszy maturalnych |
3 |
Podstawa programowa - zakres podstawowy |
27.04.2016
środa |
Rozwiązywanie arkuszy maturalnych
Pewniaki i wskazówki - video |
3 |
Podstawa programowa - zakres podstawowy |
29.04.2016
piątek |
Zakończenie roku szkolenego 2015/2016 |
|
|
V - STEREOMETRIA |
23
godziny |
P - zakres podsstawowy,
R- zakres rozszerzony |
04.01.2016
poniedziałek |
1. Proste i płaszczyzny w przestrzeni
Kryteria sukcesu:
Potrafię określać wielościany i ich własności;
Potrafię wskazywać w wielościanach proste prostopadłe, równoległe i skośne;
Potrafię wskazywać w wielościanach rzut prostokątny danego odcinka;
Potrafię przeprowadzać wnioskowania dotyczące położenia prostych w przestrzeni;
Podręcznik: MATeMAtyka str. 146, 147, 148
lub e-podrecznik STEREOMETRIA - str. 3,4,5,6,7
www.mojezadanie.pl kod dotępu: kd4the
Proste i płaszczyzny w przestrzeni |
1 |
|
08.01.2016
piątek
11.01.2016
poniedziałek |
2. Graniastosłupy - rodzaje, siatki i pole powierzchni
Kryteria sukcesu:
Potrafię określać liczbę ścian, wierzchołków i krawędzi graniastosłupów;
Potrafię sporządzać rysunek graniastosłupa wraz z oznaczeniami; Potrafię obliczać pola powierzchni bocznej i całkowitej graniastosłupów prostych;
Potrafię rysować siatkę graniastosłupa prostego, mając dany jej fragment;
Potrafię sprawdzać wzór Eulera w odniesieniu do wybranych graniastosłupów;
Potrafię obliczać długości przekątnych graniastosłupów prostych; Potrafię stosować definicje i własności funkcji trygonometrycznych do obliczania pól powierzchni graniastosłupów;
www.mojezadanie.pl kod dostępu: g4the
Rodzaje graniastosłupów,
Siatki prostopadłościanów i graniastosłupów-video |
2 |
P - Uczeń stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości.
|
11.01.2016
poniedziałek |
3. Odcinki i kąty w graniastosłupach
Kryteria sukcesu:
Potrafię sporządzać rysunek graniastosłupa wraz z oznaczeniami;
Potrafię obliczać długości przekątnych graniastosłupów prostych;
Potrafię stosować definicje i własności funkcji trygonometrycznych do obliczania pól powierzchni graniastosłupów.
Odcinki w graniastosłupach |
2 |
P - Uczeń rozpoznaje w graniastosłupach kąty między odcinkami (np. krawędziami, krawędziami i przekątnymi, itp.), oblicza miary tych kątów;
P - Uczeń stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości. |
13.01.2016
sroda + kart. |
4. Objętość graniastosłupa
Kryteria sukcesu:
Potrafię obliczać objętości graniastosłupów prostych;
Potrafię stosować definicje i własności funkcji trygonometrycznych do obliczania objętości graniastosłupów;
Potrafię rozwiązywać zadania o kontekście praktycznym dotyczące graniastosłupów.
Objętość i pole powierzcni w graniastosłupach |
2 |
P - Uczeńrozpoznaje w graniastosłupach i ostrosłupach kąty między odcinkami (np. krawędziami, krawędziami i przekątnymi, itp.), oblicza miary tych kątów;
P - Uczeń stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości. |
13.01.2016
sroda
15.01.2016
piątek |
5. Ostrosłupy - rodzaje, siatki i pole powierzchni
Kryteria sukcesu:
Potrafię sporządzić rysunek ostrosłupa wraz z oznaczeniami; Potrafię obliczać pole powierzchni ostrosłupa, mając daną jego siatkę;
Potrafię rysować siatkę ostrosłupa prostego, mając dany jej fragment;
Potrafię obliczać pola powierzchni bocznej i całkowitej ostrosłupów;
Potrafię stosować definicje i własności funkcji trygonometrycznych do obliczania pól powierzchni ostrosłupów
www.mojezadanie.pl kod dostępu: o4the |
2 |
P - Uczeń stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości. |
15.01.2016
piątek
18.01.2016
poniedziałek+ kart. |
6. Objętość ostrosłupa
Kryteria sukcesu:
Potrafię obliczać objętości ostrosłupów prawidłowych
Potrafię stosować definicje i własności funkcji trygonometrycznych do obliczania objętości ostrosłupów;
Potrafię rozwiązywać zadania o podwyższonym stopniu trudności dotyczące ostrosłupów , zadania o kontekście realistycznym
Wszystko o ostrosłupach - video |
2 |
P - Uczeń stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości. |
18.01.2016
poniedziałek |
7. Kąt między prostą a płaszczyzną, Kąt dwuścienny, Przekroje wielościanów
Kryteria sukcesu:
Potrafię wskazywać kąt między przekątną graniastosłupa a płaszczyzną podstawy tego graniastosłupa
Potrafię wyznaczać kąt między przekątną graniastosłupa a płaszczyzną podstawy tego graniastosłupa;
Potrafię wskazywać kąt między danym odcinkiem w ostrosłupie a płaszczyzną podstawy tego ostrosłupa;
Potrafię wyznaczać kąt między danym odcinkiem w ostrosłupie a płaszczyzną podstawy tego ostrosłupa;
Potrafię wskazywać kąt między sąsiednimi ścianami wielościanów;
Potrafię wyznaczać kąt między sąsiednimi ścianami wielościanów;
Potrafię rozwiązywać zadania z wykorzystaniem miary kąta między prostą a płaszczyzną, miary kąta dwuściennego. |
2 |
P - Uczeń rozpoznaje w graniastosłupach i ostrosłupach kąt między odcinkami i płaszczyznami (między krawędziami i ścianami, przekątnymi i ścianami), oblicza miary tych kątów;
P - Uczeń rozpoznaje w graniastosłupach i ostrosłupach kąty między ścianami;
P - Uczeń określa, jaką figurą jest dany przekrój prostopadłościanu płaszczyzną;
R - Uczeń określa, jaką figurą jest dany przekrój graniastosłupa lub ostrosłupa płaszczyzną. |
20.01.2016
sroda |
8. Walec
Kryteria sukcesu:
Potrafię sporządzić rysunek walca wraz z oznaczeniami;
Potrafię obliczać pole powierzchni całkowitej walca;
Potrafię zaznaczać przekrój osiowy walca;
Potrafię obliczać objętość walca;
Potrafię stosować definicje i własności funkcji trygonometrycznych do obliczania pola powierzchni i objętości walca;
Potrafię rozwiązywać zadania o podwyższonym stopniu trudności dotyczące walca;
zadanie - video
www.mojezadanie.pl kod dostępu: w4the |
2 |
P - Uczeń rozpoznaje w walcach i w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między tworzącą a podstawą), oblicza miary tych kątów;
P - Uczeń stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości. |
20.01.2016
sroda
22.01.2016
piątek+ kart. |
9. Stożek
Kryteria sukcesu:
Potrafię sporządzić rysunek stożka wraz z oznaczeniami
Potrafię obliczać pole powierzchni całkowitej stożka;
Potrafię zaznaczać przekrój osiowy i kąt rozwarcia stożka
Potrafię obliczać objętość stożka;
Potrafię rozwiązywać zadania dotyczące rozwinięcia powierzchni bocznej stożka;
Potrafię stosować definicje i własności funkcji trygonometrycznych do obliczania pola powierzchni i objętości stożka;
Potrafię rozwiązywać zadania o podwyższonym stopniu trudności dotyczące stożka;
zadanie - video; zadanie2 - video
zadanie maturalne-
www.mojezadanie.pl kod dostępu: s4the |
2 |
P - Uczeń rozpoznaje w walcach i w stożkach kąt między odcinkami oraz kąt między odcinkami i płaszczyznami (np. kąt rozwarcia stożka, kąt między tworzącą a podstawą), oblicza miary tych kątów;
P - Uczeń stosuje trygonometrię do obliczeń długości odcinków, miar kątów, pól powierzchni i objętości. |
22.01.2016
piątek |
10. Kula
Kryteria sukcesu:
Potrafię sporządzić rysunek kuli wraz z oznaczeniami,
zaznaczać koło wielkie;
Potrafię obliczać pole powierzchni kuli i jej objętość;
Potrafię rozwiązywać zadania o podwyższonym stopniu trudności dotyczące kuli.
zadanie-video zadanie2-video
www.mojezadanie.pl kod dostępu: k4the |
1 |
R - Uczeń określa, jaką figurą jest dany przekrój sfery płaszczyzną;
P - Uczeń oblicz pole powierzchni i objętość. |
25.01.2016
poniedziałek |
11. Bryły podobne
Kryteria sukcesu:
Potrafię wyznaczać skalę podobieństwa brył podobnych;
Potrafię wykorzystywać podobieństwo brył do obliczania objętości |
1 |
|
25.01.2016
poniedziałek |
12. Powtórzenie wiadomości
Kryteria sukcesu:
jak wyzej
Przygotowanie do pracy klasowej - plik pdf
polecam zadania strona pomoce linki - stereometria
|
2 |
jak wyżej |
27.01.2016
środa
29.01.2016
piątek |
13. Praca klasowa i jej omówienie |
2 |
|
| |
|
|
|
I SEMESTR ROK SZKOLNY 2015/2016 |
I - NA DOBRY START - ważne podstawy - POWTÓRZENIE
|
11 |
|
2.09.2015
środa |
1. Zapoznanie z zakresem programu w klasie 4, zasadami pracy na lekcji i prac samodzielnych. Przedstawienie PSO. |
1 |
P-Uczeń zna program w klasie 4, wymagania oraz PSO. |
2.09.2015
środa |
2. Wyrażenia arytmetyczne, kolejność działań.
Kryteria sukcesu:
- Znam zasadę kolejności wykonywania działań;
- Potrafię dodawać, odejmować, mnożyć, dzielić liczby wymierne; |
1 |
P-Uczeń potrafi obliczyć wartość wyrażenia arytmetycznego; |
3.09.2015
czwartek |
3. Działania na potęgach i pierwiastkach
Kryteria sukcesu:
- Potrafię obliczać potęgi o wykładnikach całkowitych;
- Znam prawa działań na potęgach;
- Potrafię obliczać potęgi o wykładnikach całkowitych;
- Znam pojęcie pierwiastka arytmetycznego z liczby nieujemnej
- Potrafię stosować prawa działań na pierwiastkach w obliczeniach;
- Potrafię obliczyć pierwiastki stopnia nieparzystego z liczb ujemnych.
Tu link --> Spradź czy już potrafisz
Działania na pierwiastkach |
1 |
P-Uczeń posługuje się w obliczeniach pierwiastkami dowolnego stopnia i stosuje prawa działań na pierwiastkach;
Uczeń oblicza potęgi o wykładnikach wymiernych i stosuje prawa działań na potęgach o wykładnikach wymiernych;
|
9.09.2015
środa |
4. Wyrażenia algebraiczne - wzory skróconego mnożenia
Kryteria sukcesu:
- Potrafię sprawnie posługiwać się wzorami skróconego mnożenia:
i sprawnie wykonuje działania na wyrażeniach algebraicznych, które zawierają wymienione wzory skróconego mnożenia;
przykład 1
przykład 2
SPRAWDŹ CZY UMIESZ |
1 |
P-Uczeń używa wzorów skróconego mnożenia na
|
9.09.2015
środa |
5. Działania na liczbach niewymiernych
Kryteria sukcesu:
- Potrafię sprawnie posługiwać się wzorami skróconego mnożenia.
- Potrafię wykonać działania na liczbach niewymiernych, które zawierają wzory skróconego mnożenia;
przykład
- Potrafię usunąć niewymierność z mianownika.
Przykład
Potrafię przeprowadzać działania na liczbach niewymiernych
Przykład |
1 |
P-Uczeń używa wzorów skróconego mnożenia na
 |
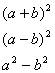10.09.2015
czwartek |
6. Równania i nierówności pierwszego stopnia
Kryteria sukcesu:
- Potrafię sprawdzić czy dana liczba jest rozwiązaniem równania bądź nierówności.
- Potrafię rozwiązać równanie i nierówność pierwszego stopnia z jedną niewiadomą.
przykład - powtórzenie - równania
przykład 2 - nierówność
zadanie domowe - nierówności |
1 |
P-Uczeń sprawdza, czy dana liczba rzeczywista jest rozwiązaniem równania lub nierówności;
Uczeń rozwiązuje nierówności pierwszego stopnia z jedną niewiadomą; |
14.09.2015
poniedziałek |
7. Równania kwadratowe
Kryteria sukcesu:
Potrafię odróżnić równanie kwadratowe od innych równań.
Potrafię obliczyć wyróżnik równania kwadratowego.
Potrafię określić ile rozwiązań ma równanie kwadratowe.
Potrafię rozwiązać równanie kwadratowe.
tutaj powtórzysz równania kwadratowe - zadanie domowe |
1 |
P-Uczeń rozwiązuje równania kwadratowe z jedną niewiadomą; |
16.09.2015
środa
16.09.2015
środa |
8. Nierówności kwadratowe
Kryteria sukcesu:
Potrafię rozwiązać nierówność kwadratową.
Potrafię określić zbiór rozwiązań nierówności kwadratowej i zaznaczyć rozwiązanie na osi liczbowej oraz zapisać w postaci symbolicznej.
tutaj powtórzysz nierówności kwadratowe
nierówności kwadratowe w innym wydaniu - ćwicz warto!!! |
2 |
P-Uczeń rozwiązuje nierówności kwadratowe z jedną niewiadomą; |
17.09.2015
czwartek |
9. Równania wielomianowe i wymierne
Kryteria sukcesu:
Potrafię podać rozwiązania wielomianu przedstawionego w postaci iloczynu 
Sprawdź czy umiesz?
Potrafię rozwiązać równania typu:
 |
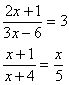1 |
P-Uczeń korzysta z własności iloczynu przy rozwiązywaniu równań typu:
P-Uczeń: rozwiązuje proste równania wymierne, prowadzące do równań liniowych lub kwadratowych, np.
 |
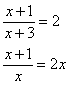21.09.2015
poniedziałek |
10. Sprawdzian - na dobry start - PRZYKŁADY NA SPRAWDZIAN |
1 |
uczeń rozwiązuje zadania zgodnie z wymaganiami określonymi w kryteriach sukcesu |
II |
Funkcje wykładnicze i logarytmiczne |
22 godziny |
P - zakres podsstawowy,
R- zakres rozszerzony |
23.09.2015
środa (2h)
24.09.2015
czwartek |
1. Potęga o wykładniku wymiernym
Kryteria sukcesu:
Znam własność potęgi o wykładniku wymiernym:  ;  jeśli a>0 , n jest liczbą naturalną, m jest liczbą całowitą.
Potrafię obliczać wartości poteg o wykładniku wymiernym
Potrafię stosować prawa działań na potęgach i pierwiastkach
Potęga o wykładniku wymiernym-teoria i zastosowanie
Przykłady potega o wykładniku wymiernym (video)
Wykład o działaniach na potegach o wykładniku wymiernym |
3 |
P- uczeń oblicza potęgi o wykładnikach wymiernych istosuje prawa działań na potęgach o wykładnikach wymiernych;
P- uczeń wykorzystuje podstawowe własności potęg |
28.09.2015
poniedziałek |
2. Potęga o wykładniku rzeczywistym
Kryteria sukcesu:
Potrafię obliczać wartości poteg o wykładniku wymiernym i niewymiernym.
Potrafię korzystać z kalkulatora do tych obliczeń
Potęga o wykładniku rzeczywistym
TU LINK DO PRZYKŁADÓW NA KARTKÓWKĘ - ćwicz swoje umiejetności.
(PONIEDZIAŁEK - 28.09.2015) Tu pobierz plik pdf z przykładami - rozwiąż i sprawdź rozwiązania |
1 |
P-uczeń oblicza potęgi o wykładnikach wymiernych istosuje prawa działań na potęgach o wykładnikach wymiernych;
P- uczeń wykorzystuje podstawowe własności potęg |
30.09.2015
środa (1h) |
3. Wykres funkcji wykładniczej
Kryteria sukcesu:
Potrafię szkicować wykres funkcji  w zalezności od podstawy.
wykres funkcji 
Funkcje wykładnicze |
1 |
P-uczeń szkicuje wykresy funkcji wykładniczych dla różnych podstaw;
|
30.09.2015
środa (1h)
01.10.2015
czwartek |
4. Przekształcenia wykresu funkcji wykładniczej. Własności funkcji wykładnieczej.
Kryteria sukcesu:
Rozpoznaję wykresy funkcji wykładniczych
Potrafię na podstawie wykresu funkcji y =f(x) szkicować wykresy funkcji y = f(x + a), y = f(x)+ a,
y = –f(x), y =f(–x);
Potrafię odczytać własności funkcji z wykresu.
zadanie
Funkcje wykładnicze
Prezentacja z lekcji - WYKRSY FUNKCJI WYKŁADNICZEJ |
2 |
P-uczeń na podstawie wykresu funkcji y =f(x) szkicuje wykresy funkcji
y = f(x + a), y = f(x)+ a,
y = –f(x), y =f(–x);
R-uczeń na podstawie wykresu funkcji y = f(x) szkicuje wykresy funkcji:
y = |f(x)|, y = c ·f(x), y = f(cx);
R -uczeń szkicuje wykres funkcji określonej w różnych przedziałach różnymi wzorami; odczytuje własności takiej funkcji z wykresu. |
05.10.2015
poniedziałek |
6. Logarytm
Kryteria sukcesu:
Znam definicję logarytmu i potrafię ja stosować do obliczeń
Zadania cz I, zadania czII
Sprawdź czy umiesz? Elementarne równanie wykładnicze i wykorzystanie potęgi - ćwiczenia wspomagjace obliczanie logarytmów.
Logarytmy najwazniejsze wiadomości
Prezentacja z lekcji - LOGARYTM
Zadanie domowe |
1 |
P- uczeń wykorzystuje definicję logarytmu |
07.10.2015
środa (2h)
08.10.2015
czwartek |
7. Własności logarytmów
Kryteria sukcesu:
Znam wzory na logarytm iloczynu, logarytm ilorazu i logarytm potęgi o wykładniku naturalnym i potrafię je stosować do obliczeń
Zadania-video
Wszystko o logarytmach-video
SPRAWDŹ CZY UMIESZ?
Prezentacja z lekcji - własności logarytmów (sroda)
Prezentacja z lekcji (czwartek)własności logarytmów
Zadanie domowe na poniedziałek- plik pdf
Po tej lekcji planowana jest kartkówka z logarytmów
PRZYKŁADY NA KARTKÓWKĘ - LOGARYTMY - na poniedziałek 12.10.2015 |
3 |
P- uczeń wykorzystuje definicję logarytmu i stosuje w obliczeniach wzory na logarytm iloczynu, logarytm ilorazu i logarytm potęgi o wykładniku naturalnym;
|
12.10.2015
poniedziałek |
8. Funkcje logarytmiczne - wykresy
Kryteria sukcesu:
Potrafię szkicować wykres funkcji 
w zalezności od podstawy.
Przykłady-video Prezentacja z lekcji |
1 |
R-uczeń szkicuje wykresy funkcji logarytmicznych dla
różnych podstaw; |
15.10.2015
czwartek
19.10.2015
poniedziałek |
9. Przekształcenia wykresu funkcji logarytmicznej
Kryteria sukcesu:
Potrafię szkicować wykres funkcji logarytmicznej zgodnie z podanym wzorem.
Funkcja logarytmiczna i jej przesuniecia o wektor - video
Ptrzentacja z lekcji |
2 |
P-uczeń na podstawie wykresu funkcji y =f(x) szkicuje wykresy funkcji
y = f(x + a), y = f(x)+ a,
y = –f(x), y =f(–x);
R-uczeń na podstawie wykresu funkcji y = f(x) szkicuje wykresy funkcji
y = |f(x)|, y = c ·f(x), y = f(cx); |
21.10.2015
środa (2h) |
10. Zmiana podstawy logarytmu
Kryteria sukcesu:
Znam twierdzenie o zamianie logarytmów i potrafię je stosować do obliczeń logarytmicznych
a, b, x >0 oraz  i  to:
 Przykłady
Zadanie domowe zadanie 3 str 117
Zadanie domowe zadanie 1 str 128
Zadanie domowe zadanie 4 str 129
Prezentacja z lekcji |
2 |
R-uczeń stosuje w obliczeniach wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu. |
22.10.2015
czwartek
26.10.2015
poniedziałek
28.10.2015
środa (1h) |
11. Funkcje wykładnicze i logarytmiczne – zastosowania
Zadanie z fizyki z zastosowaniem funkcji wykładniczej
Zadanie z fizyki z zastosowaniem funkcji wykładniczej
Zadanie na zastosowanie funkcji wykadniczej
Logarytm i skala logarytmiczna - zastosowanie
Logarytm na kalkulatorze
Zastosowanie funkcji wykładniczej - praktycznie-prezentacja prezi |
3 |
P-posługuje się funkcjami wykładniczymi do opisu zjawisk fizycznych, chemicznych, a także w zagadnieniach osadzonych w kontekście praktycznym.
R- uczeń wykorzystuje podstawowe własności potęg (również w zagadnieniach związanych z innymi dziedzinami wiedzy, np. fizyką, chemią, informatyką);
R-uczeń posługuje się funkcjami logarytmicznymi do opisu zjawisk fizycznych, chemicznych, a także w
zagadnieniach osadzonych w kontekście praktycznym; |
28.10.2015
środa (1h) |
12. Powtórzenie wiadomości
Przykładowe zadania na pracę klasową podane według kryteriów sukcesu. - plik pdf
Rozwiązania zadań |
1 |
kryteria sukcesu na prcę klasową-pdf |
29.10.2015
czwartek
02.11.2015
poniedziałek |
13. Praca klasowa i jej omówienie
Zadania z pracy klasowej i ich przykładowe rozwiązania |
2 |
j.w |
III |
Rachunek prawodpodobieństwa |
20 godzin |
G - zakres gimnazjum
P - zakres podsstawowy,
R- zakres rozszerzony |
04.11.2015
środa
2h |
1. Reguła mnożenia i reguła dodawania
Kryteria sukcesu:
Znam zasadę reguły mnozenia i regułę dodawania;
Stosuje regułę mnożenia w sytuacjach typowych;
Zliczam ilość wyników sprzyjających zdarzeniu w prostych przypadkach;
Zasada mnożenia - video
Film godny uwagi z działu kombinatoryki - zobacz koniecznie - video
Prezentacja z lekcji - wstęp do kombinatoryki - reguła mnożenia i dodawania |
2 |
P-uczeń:zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania |
05.11.2015
czwartek |
2. Permutacje
Kryteria sukcesu:
Używam znaku n! do obliczeń iloczynów kolejnych liczb naturalnych;
Wiem co to jest permutacja.
Do obliczeń wykorzystuję wzór na liczbę permutacje lub regułę mnożenia.
Przykłady permutacji i wariacji bez powtórzeń
Potęgowanie i silnia
Prezentacja z lekcji - Permutacje |
1 |
P-uczeń:zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania
R- uczeń: wykorzystuje wzory na liczbę permutacji, |
09.11.2015
poniedziałek |
Poprwa pracy klasowej III termin
Potęga o wykładniku wymiernym, logarytmy, funkcje wykładnicze i funkcje logarytmiczne - kryteria sukcesu jak 29.10.2015r.
Uczniowie, którzy nie poprawiają pracy klasowej, rozwiązywać będą zadania z zakresu materiału od 2.09.2015 do 06.11.2015 |
1 |
jak w dziale
Funkcje wykładnicze
i funkcje logarytmiczne |
12.11.2015
czwartek |
3. Wariacje bez powtórzeń
Kryteria sukcesu:
Potrafię podać przykład na wariacje bez powtórzeń;
Wiem kiedy stosować wariacje bez powtórzeń;
Do obliczeń wykorzystuję wzór na liczbę wariacji bez powtórzeń lub regułę mnożenia.
Przykłady permutacji i wariacji bez powtórzeń
Prezentacja z lekcji - Wariacje bez powtórzeń |
1 |
P-uczeń:zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania
R- uczeń wykorzystuje wzory na liczbę wariacji do zliczania obiektów w bardziej złożonych sytuacjach kombinatorycznych; |
16.11.2015
poniedziałek |
4. Wariacje z powtórzeniami
Kryteria sukcesu:
Znam i rozumię znaczenie pojęć: wariacje z powtórzeniami, wariacje bez powtórzeń,
Potrafię zastosować poznane pojęcia kombinatoryczne
Porządkuję i wykorzystuję informacje zawarte w treści zadania
Potrafię podać przykład na wariacje z powtórzeniami;
R-Do obliczeń wykorzystuję wzór na liczbę wariacji z powtórzeniami oraz na liczbę wariacji bez powtórzeń
P - lub stosuję regułę mnożenia.
Wariacje z powtórzeniami-video
Prezentacja z lekcji - Wariacje z powtórzeniami |
1 |
P-uczeń:zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania
R- uczeń: wykorzystuje wzory na liczbę wariacji z powtórzeniami do zliczania obiektów w bardziej złożonych sytuacjach kombinatorycznych; |
18.11.2015
środa
2h |
5. Kombinacje
Kryteria sukcesu:
Znam i rozumie znaczenie pojęcia kombinacje
Potrafię zastosować poznane pojęcia kombinatoryczne
Porządkuję i wykorzystuję informacje zawarte w treści zadania
Potrafię obliczyć ile muszę skreślić kuponów w lotto (6 z 49) aby trafić 6.
Kombinacje- przykłady - video
Podstawy kombinatoryki - video
Zadania z lekcji |
2 |
P-uczeń:zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania
R- uczeń: wykorzystuje wzory na liczbę kombinacji, do zliczania obiektów w bardziej złożonych sytuacjach kombinatorycznych; |
19.11.2015
czwartek
23.11.2015
poniedziałek |
6. Rozwiązywanie zadań z kombinatoryki
Kryteria sukcesu:
Znam i rozumie znaczenie pojęć: permutacje, wariacje bez powtórzeń, wariacje z powtórzeniami, kombinacje
Potrafię zastosować poznane pojęcia kombinatoryczne
Porządkuję i wykorzystuję informacje zawarte w treści zadania
Zadania z kombinatoryki - video
na poniedziałek planowany jest 25 minutowy sprawdzian z kombinatoryki -
tu przykładowe zadania czI
tu przykładowe zadania czII |
2 |
P-uczeń:zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania
R- uczeń: wykorzystuje wzory na liczbę permutacji, kombinacji, wariacji i wariacji z powtórzeniami do zliczania obiektów w bardziej złożonych sytuacjach kombinatorycznych; |
25.11.2015
środa 1h |
7. Zdarzenia losowe
Kryteria sukcesu:
Znam pojęcie przestrzeni zdarzeń elementarnych,
Znam pojęcie zdarzenia losowego,
Potrafię wyznaczyć zbiór wszystkich zdarzeń elementarnych;
Potrafię wyznaczać zbiór zdarzeń elementarnych sprzyjających danemu zdarzeniu losowemu oraz potrafię określić liczbę tych zdarzeń;
Staram się czytać tekst matematyczny ze zrozumieniem.
rzuty kostką - zdarzenia losowe |
1 |
G- uczeń analizuje proste doświadczenia losowe |
25.11.2015
środa 1h
30.11.2015
poniedziałek
02.12.2015
|
8. Prawdopodobieństwo klasyczne.
Kryteria sukcesu:
Znam klasyczną definicję prawdopodobieństwa
Potrafię zastosować klasyczną definicję prawdopodobieństwa
Rzwiązuję proste zadania z prawdopodobieństwa
co to jest prawdopodobieństwo - video
Rachunek prawdopodobieństwa i kombinatoryka - najważniejsze wiadomości |
4 |
P- uczeń:oblicza prawdopodobieństwa w prostych sytuacjach, stosując klasyczną definicję prawdopodobieństwa. |
03.12.2015
czwartek
|
9. Własności prawdopodobieństwa
Prawdopodobieństwo warunkowe i całkowite.
Kryteria sukcesu:
Znam własności prawdopodobieństwa
Wiem jak obliczyć sumę prawdopodobieństw
Wiem co to jest prawdopodobieństwo warunkowe
Znam wzór na prawdopodobieństwo warunkowe i całkowite.
Prezentacja z lekcji
Prawdopodobienstwo warunkowe-video |
1 |
R- uczeń: oblicza prawdopodobieństwo warunkowe;
R -uczeń: korzysta z twierdzenia
o prawdopodobieństwie całkowitym |
07.12.2015
poniedziałek |
10. Doświadczenia wieloetapowe
Kryteria sukcesu:
Potrafię obliczać prawdopodobieństwo zdarzenia doświadczenia wieloetapowego
Potrafię interpretować wieloetapowe doświadczenie za pomocą drzewa.
Obliczam prawdopodobieństwo zdarzenia za pomocą drzewka.
Prezentacja z lekcji |
1 |
P-uczeń:zlicza obiekty w prostych sytuacjach kombinatorycznych, niewymagających użycia wzorów kombinatorycznych, stosuje regułę mnożenia i regułę dodawania
R- uczeń: wykorzystuje wzory na liczbę permutacji, kombinacji, wariacji i wariacji z powtórzeniami do zliczania obiektów w bardziej złożonych sytuacjach kombinatorycznych; |
09.12.2015
środa |
11. Przygotowanie do pracy klasowej
Kryteria sukcesu jak wyżej
Przykładowe zadania na pracę klasową - plik pdf
|
1 |
jak wyżej |
10.12.2015
czwartek
14.12.2015
poniedziałek |
12. Praca klasowa i jej omówienie
Kryteria sukcesu:
jak wyżej |
2 |
jak wyżej |
IV |
Statystyka |
7 godzin |
G- zakres gimnazjum
P - zakres podsstawowy,
R- zakres rozszerzony |
09.12.2015
środa
|
1. Średnia arytmetyczna
Kryteria sukcesu:
Obliczam średnią arytmetyczną skończonego zbioru danych.
Interpretuję otrzymaną średnią arytmetyczną.
Potrafię obliczać średnią arytmetyczną danych przedstawionych na diagramie.
Potrafię wykorzystywać średnią arytmetyczną do rozwiązywania zadań .
Rozwiązuję zadania, w których wykorzystuję definicje średniej
arytmetycznej.
Prezentacja z lekcji- zadania
Polecam ćwiczenia interaktywne - srednia arytmetyczna
Jak obliczyć średnią arytmetyczną?
Zadanie domowe
www.mojezadanie.pl kod dostepu: ds4the |
1 |
G- uczeń: wyznacza średnią arytmetyczną zestawu danych; |
16.12.2015
środa |
2. Mediana i dominanta, średnia arytnetyczna - interpretacje
Kryteria sukcesu:
Rozróżniam pojęcia mediany i mody
Obliczam medianę i modę skończonego zbioru danych.
Rozwiązuję zadania, w których wykorzystuje definicje średniej
arytmetycznej,mediany i mody.
Jak policzyć dominantę? - video
Jak obliczyć medianę? - video |
2 |
G- uczeń zna pojęcie dominanty i mediany interpretuje te parametry dla danych empirycznych;
G - wyznacza medianę zestawu danych; |
21.12.2015
poniedziałek
|
3. Odchylenie standardowe
Kryteria sukcesu:
Znam pojęcia wariancji i odchylenia standardowego skończonego zbioru danych.
Obliczam wariancję i odchylenie standardowe.
Interpretuję wariancję i odchylenie standardowe.
Wyznaczam rozstęp danych liczbowych.
Potrafię obliczać wariancję i odchylenie standardowe danych i je interpretować
Potrafię obliczać wariancję i odchylenie standardowe danych przedstawionych w tabeli lub na diagramie.
Jak obliczyć odchylenie standardowe?
odchylenie standardowe - przykład - video |
1 |
P- oblicza odchylenie
standardowe zestawu danych (także
w przypadku danych odpowiednio
pogrupowanych), interpretuje te parametry dla danych empirycznych; |
17.12.2015
czwartek |
4. Średnia ważona
Kryteria sukcesu:
Obliczam średnią ważoną skończonego zbioru danych.
Interpretuję otrzymaną średnią arytmetyczną i średnią ważoną.
Obliczam średnie, gdy dane są odpowiednio pogrupowane
Rozwiązuję zadania, w których wykorzystuje definicje średniej
arytmetycznej, średniej ważonej.
Powtórzenie - video- Statystyka: mediana, dominanta, wariancja, średnia ważona, odchylenie standdardowe |
1 |
P- oblicza średnią ważoną zestawu danych (także w przypadku danych odpowiednio pogrupowanych), interpretuje te parametry dla danych empirycznych; |
04.01.2016
poniedziałek |
5 Rozwiązywanie zadań - statystyka
Kryteria sukcesu:
Rozwiązuję zadania, w których wykorzystuje definicje średniej
arytmetycznej, średniej ważonej. mediany, dominanty, średniej ważonej i odchylenia standardowego.
Interpretuje w/w parametry dla danych empirycznych.
Karta pracy na lekcji
Polecane video - dotyczace poznanych pojęć |
2 |
P- oblicza średnią ważoną zestawu danych (także w przypadku danych odpowiednio pogrupowanych), interpretuje te parametry dla danych empirycznych;
P-oblicza odchylenie
standardowe zestawu danych interpretuje te parametry dla danych empirycznych; |
08.01.2016
piątek |
6. Sprawdzian-statystyka
Rozwiązuję zadania tekstowe na obliczanie średniej arytmetycznej, średniej wazonej,mediany i odchylenia standardowego. |
1 |
jak wyżej |
Pozostałe działy matematyki w klasie 4 THE |
| |
SZCZEGÓŁOWE ROZKŁADY TEMATÓW LEKCJI WKRÓTCE
|
VII |
Powtórzenie przed maturą |
44
godzin |
RAZEM GODZIN W ROKU SZKOLNYM 2015/2016
|
164 |
|
;){kind=link}
;){kind=link}
;){kind=link}
;){kind=link}